BÚSQUEDA ENTRE ADVERSARIOS

ESCUELA SUPERIOR POLITÉCNICA AGROPECUARIA DE MANABÍ

MANUEL FÉLIX LÓPEZ

CARRERA INFORMÁTICA

    SEMESTRE  SÉPTIMO           PERIODO  ABR 2015/SEP 2015

TEMA:

BÚSQUEDA ENTRE ADVERSARIOS

MATERIA:

INTELIGENCIA ARTIFICIAL II

AUTOR:

CARLOS A. ZAMBRANO VIDAL

FACILITADORA:

ING. HIRAIDA SANTANA

CALCETA,  JULIO 2015

INTRODUCCIÓN

Bueno hasta ahora solo hemos visto estrategias en las que un solo agente busca la solución a un problema. Existen otro tipo de problemas en los que dos agentes compiten por un mismo objetivo. Este es el caso de la búsqueda con adversarios, ya que este trata de saber cuál es el mejor movimiento a efectuar, pero teniendo en cuenta toda la dinámica del juego (todo lo que ocurrirá si se hace ese movimiento).

MARCO TEÓRICO

BÚSQUEDA ENTRE ADVERSARIOS

JUEGOS

En los entornos multiagente (cooperativos o competitivos), cualquier agente tiene que considerar las acciones de otros agentes. La imprevisibilidad de estos otros agentes puede introducir muchas contingencias en el proceso de resolución de problemas. Los entornos competitivos, en los cuales los objetivos de los agentes están en conflicto, dan ocasión a problemas de búsqueda entre adversarios, a menudo conocidos como juegos. La teoría matemática de juegos, una rama de la economía, ve a cualquier entorno multiagente como un juego. En Inteligencia Artificial, los “juegos” son una clase más especializada, que los teóricos llaman juegos:

Ø  De suma cero.

Ø  De dos jugadores (jugador MAX, jugador MIN).

Ø  Por turnos.

Ø  Deterministas.

Ø  De información perfecta (ajedrez, damas, tres en raya...) vs. Información imperfecta (poker, stratego, bridge...).

Los juegos son interesantes porque son demasiado difíciles de resolver.

Los entornos competitivos, en los cuales los objetivos del agente están en conflicto, dan ocasión a problemas de búsqueda entre adversarios, a menudo conocido como juegos.

La manera natural de responder un juego es mediante un árbol de juegos que es un tipo especial de árbol semántico en los que los nodos representan configuraciones de tableros y las ramas indican como una configuración puede transformarse en otra mediante un solo movimiento.

DECISIONES ÓPTIMAS EN JUEGOS

Un juego puede definirse formalmente como una clase de problemas de búsqueda con los componentes siguientes:

Ø  El estado inicial.

Ø  Una función sucesor, que devuelve una lista de pares (movimiento, estado).

Ø  Un test terminal, que determina cuándo termina el juego (por estructura o propiedades o función utilidad).

Ø Una función utilidad

ALGORITMO MINIMAX

Es un método de decisión para minimizar la pérdida máxima esperada en juegos con adversario. Como es imposible hacer una exploración exhaustiva de todas las jugadas, se hace una búsqueda limitada en profundidad.

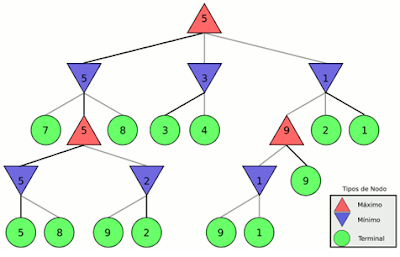
Calcula la decisión minimax del estado actual. Usa un cálculo simple recurrente de los valores minimax de cada estado sucesor. La recursión avanza hacia las hojas del árbol. Los valores minimax retroceden por el árbol cuando la recursión se va deshaciendo.

CONCLUSIÓN

Hemos analizado este tipo de búsqueda y se llega a la conclusión de que este método debemos de conocerlo muy a fondo ya que no sirve de mucho para cuando tengamos un contrincante al frente saber en qué momento y lugar hacer la jugada o movimiento preciso para ganar la partida, como la palabra mismo lo dice adversarios siempre vamos a tener a alguien con el que vamos a jugar para decidir cuál es el mejor en el juego que se está realizando.

También nos enseña a cómo defendernos en caso de enfrentarnos a un oponente sabiendo que debemos de utilizar nuestros mejores movimientos y técnicas para vencerlo.

BIBLIOGRAFÍA

Malagón, s.2010.busqueda heurísticas. (En línea).Disponible en http://www.nebrija.es/~cmalagon/ia/transparencias/busqueda_heuristica.pdf

Russell, s.2008.inteligencia artificial un enfoque moderno. Segunda edición. Pearson education. Madrid-España.